Equations for Single-Phase Porous Media Flow
- Introduction :
The flow of a single, compressible fluid through porous,
permeable rock can be described using a partial differential equation known as
the diffusivity equation. Modified forms of the diffusivity equation can be
used to describe gas flow. A similar equation can be derived for multiphase
flow as well, and that equation is the basis for reservoir simulation. Clearly,
the diffusivity equation is at the very heart of reservoir engineering and an
intuitive understanding of this equation is essential to all who would do reservoir
engineering.
- The Conservation Equation :
Many physical systems – ranging from solar collectors to
river deltas to flow in reservoirs – can be analyzed using the principle of
conservation. This principle is closely related to the idea of a control volume
in thermodynamics; it is based on the idea that the amount of “stuff” (energy,
mass, whatever) entering, leaving, created, and destroyed in a given volume
must be balanced. We will derive the conservation equation for a radial flow
geometry, because this geometry is especially useful for well testing and
inflow analysis. We could do it for any geometry we chose.
Consider a cylindrical shell of radius r and thickness Dr (Figure 6.1).
Equation (6.4) is the conservation equation in radial
coordinates. It states that the sum of the partial differential derivatives in r and t is zero. This is also known as a divergence equation; all
conservation equations (for any quantity, in any coordinate system) can be
expressed in a form very similar to Equation 6.4.
This equation must be manipulated further to be useful: it
includes dependent variables r, f, and u, whereas we really want an equation in p only. We will use constitutive equations for these quantities to
get the desired equation.
- Use
of Darcy’s Law in the Conservation Equation
Although Equation (6.10) is in pressure, it is nonlinear. It is very difficult to solve
nonlinear partial differential equations, and we therefore seek a simplified,
linear form to work with. The nonlinearity comes from two different
sources.



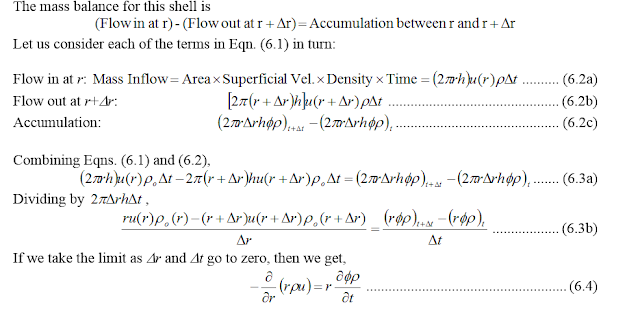















No comments:
Post a Comment